순열과 조합 - N개 중 M개를 뽑는 Case
{1, 2, 3, 4, 5} 중 3개를 뽑는 Case에 대해 알아보자
순열
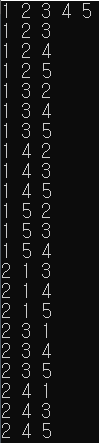
순서에 상관이 있고 중복을 허용하지 않고 나올 수 있는 모든 수열
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;
int arr[5] = { 1, 2, 3, 4, 5 };
bool check[5]; // 중복된 값을 선택하지 않기 위한 배열
int temp[3]; // 5개 중 3개를 뽑은 순열
void dfs(int x) {
if (x >= 3) {
for (int i = 0; i < 3; i++) {
cout << temp[i] << " ";
}
cout << endl;
}
else {
for (int i = 0; i < 5; i++) { // 순서에 상관이 있기 때문에 idx 0부터 시작
if (check[i] == false) {
check[i] = true;
temp[x] = arr[i];
dfs(x + 1);
check[i] = false;
temp[x] = 0;
}
}
}
}
int main() {
dfs(0);
return 0;
}
조합
순서에 상관 없이 중복을 허용하지 않고 나올 수 있는 모든 순열
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;
int arr[5] = { 1, 2, 3, 4, 5 };
int temp[3]; // 5개 중 3개를 뽑은 순열
void dfs(int x, int from) {
if (x >= 3) {
for (int i = 0; i < 3; i++) {
cout << temp[i] << " ";
}
cout << endl;
}
else {
for (int i = from; i < 5; i++) { // 순서에 없기 때문에 idx 0부터 돌지 않음(check 배열도 불필요)
temp[x] = arr[i];
dfs(x + 1, i + 1);
temp[x] = 0;
}
}
}
int main() {
for (int i = 0; i < 5; i++) {
cout << arr[i] << " ";
}
cout << endl;
dfs(0, 0);
return 0;
}
부분 집합 - N개의 원소로 이루어진 집합의 부분 집합
| 1 << 4 = 10000(16) 1 << 3 = 1000(8) 따라서 1 << n 은 2 ^ n 이라고 할 수 있다. |
{A, B, C}의 부분집합은 다음과 같이 표현할 수 있다.
i
↓
0. 0 0 0, {}
1. 0 0 1, {C}
2. 0 1 0, {B}
3. 0 1 1, {B, C}
4. 1 0 0, {A}
5. 1 0 1, {A, C}
6. 1 1 0, {A, B}
7. 1 1 1, {A, B, C}

#include <iostream>
using namespace std;
int arr[3] = { 1, 2, 3 };
void powerset(int n) {
int max = 1 << n; // 2 ^ n
for (int i = 0; i < max; i++) {
cout << "{";
for (int j = 0; j < n; j++) {
if (i & (1 << j))
cout << arr[j];
}
cout << "}" << endl;
}
}
int main() {
powerset(3);
return 0;
}'Algorithm' 카테고리의 다른 글
| [C++][프로그래머스] 외벽 점검 - 완전탐색 (0) | 2022.01.10 |
|---|---|
| [C++][백준] 비밀 보임 (13424) - 플로이드와샬 (0) | 2021.09.14 |
| [C++][백준] 욕심쟁이 판다 (1937) - dp (0) | 2021.08.24 |
| [C++][프로그래머스] 메뉴 리뉴얼 - 비트마스크 완전탐색 (1) | 2021.07.09 |
| [C++][백준] 텀 프로젝트 (9466) - 스택 (0) | 2021.06.18 |



