[C++][프로그래머스] 징검다리
문제 설명
출발지점부터 distance만큼 떨어진 곳에 도착지점이 있습니다. 그리고 그사이에는 바위들이 놓여있습니다. 바위 중 몇 개를 제거하려고 합니다.
예를 들어, 도착지점이 25만큼 떨어져 있고, 바위가 [2, 14, 11, 21, 17] 지점에 놓여있을 때 바위 2개를 제거하면 출발지점, 도착지점, 바위 간의 거리가 아래와 같습니다.
| 제거한 바위의 위치 | 각 바위 사이의 거리 | 거리의 최솟값 |
|
[21, 17] |
[2, 9, 3, 11] |
2 |
|
[2, 21] |
[11, 3, 3, 8] |
3 |
|
[2, 11] |
[14, 3, 4, 4] |
3 |
|
[11, 21] |
[2, 12, 3, 8] |
2 |
|
[2, 14] |
[11, 6, 4, 4] |
4 |
위에서 구한 거리의 최솟값 중에 가장 큰 값은 4입니다.
출발지점부터 도착지점까지의 거리 distance, 바위들이 있는 위치를 담은 배열 rocks, 제거할 바위의 수 n이 매개변수로 주어질 때, 바위를 n개 제거한 뒤 각 지점 사이의 거리의 최솟값 중에 가장 큰 값을 return 하도록 solution 함수를 작성해주세요.
제한사항
-
도착지점까지의 거리 distance는 1 이상 1,000,000,000 이하입니다.
-
바위는 1개 이상 50,000개 이하가 있습니다.
-
n 은 1 이상 바위의 개수 이하입니다.
입출력 예
|
distance |
rocks |
n |
return |
|
25 |
[2, 14, 11, 21, 17] |
2 |
4 |
풀이
n개의 바위를 제거한 뒤 각 지점 사이의 거리의 최솟값 중에 가장 큰 값을 찾는 문제입니다.
범위가 굉장히 크면서 최솟값/최댓값을 찾는 문제는 이분탐색 아이디어를 떠올릴 수 있습니다.
해당 문제에서도 distance 범위가 굉장히 크면서 최댓값을 찾는 문제입니다.
바위의 위치가 아래와 같이 주어진다고 가정해봅시다.
[2, 14, 11, 21, 17]
이때 거리의 최솟값으로 2가 될 수 있을까요?
네 가능합니다. 바위 [21, 17] 또는 바위 [11, 21]을 제거하면 각 바위 사이의 최솟값이 2라고 예제에 설명되어있습니다.

이때 거리의 최솟값으로 3이 될 수 있을까요?
네 가능합니다. 바위 [2, 21] 또는 바위 [2, 11]을 제거하면 각 바위 사이의 최솟값이 3라고 예제에 설명되어있습니다.

이때 거리의 최솟값으로 4가 될 수 있을까요?
네 가능합니다. 바위 [2, 14] 를 제거하면 각 바위 사이의 최솟값이 4라고 예제에 설명되어있습니다.


이때 거리의 최솟값으로 5가 될 수 있을까요?
없습니다. 어떤 조합으로 바위를 2개 제어해도 거리의 최솟값은 5가 될 수 없습니다.
5가 될 수 없기에 6도, 7도, 전부 거리의 최솟값이 될 수 없습니다.
이제 조금 감이 잡히셨을것 같은데요 이분탐색을 통해 처음으로 O → X로 변하는 시점을 찾을 수 있고
그 값이 결국 거리의 최솟값들 중 최댓값이 됩니다. 예제에서는 4가 되겠네요.
그렇다면 거리의 최솟값으로 mid값이 가능한지 불가능한지 판별은 어떻게 할 수 있을까요?
예를 들어 mid가 4라고 가정해봅시다.
거리의 최솟값이 4라는 의미는 모든 거리가 최소한 4보다는 같거나 커야함을 의미합니다.


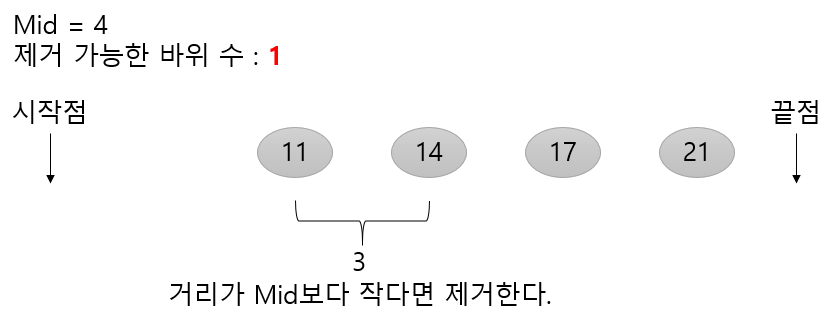
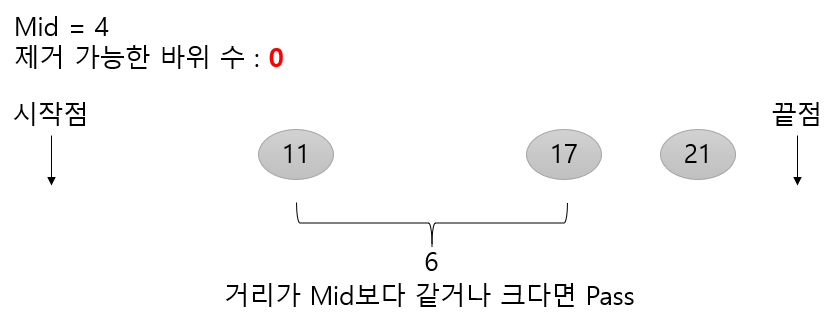


모든 rocks에 대해 다음 과정을 진행해 준뒤 제거한 바위수가 0보다 같거나 크다면 가능
제거한 바위 수가 0보다 작다면 불가능이라고 판별해주시면 됩니다.
전체 코드는 아래와 같습니다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> sortedRocks;
// 거리의 최솟값이 mid가 가능한지
bool doIt(int mid, vector<int> rocks, int n) {
int prev = 0;
int rockNum = n;
for (int i = 0; i < rocks.size(); i++) {
if (rocks[i] - prev >= mid) {
prev = rocks[i];
}
else {
rockNum--;
}
}
if (rockNum < 0) return false;
else return true;
}
int solution(int distance, vector<int> rocks, int n) {
int answer = 0;
sort(rocks.begin(), rocks.end());
int l = 1, r = distance;
while (l < r) {
int mid = (l + r) / 2;
if (!doIt(mid, rocks, n)) { // 거리의 최솟값이 mid가 가능한지
r = mid;
}
else {
l = mid + 1;
}
}
answer = r - 1;
return answer;
}
int main() {
int distance = 25;
vector<int> rocks = { 2, 14, 11, 21, 17 };
int n = 2;
cout << solution(25, rocks, n);
return 0;
}