문제
상담원으로 일하고 있는 백준이는 퇴사를 하려고 한다.
오늘부터 N+1일째 되는 날 퇴사를 하기 위해서, 남은 N일 동안 최대한 많은 상담을 하려고 한다.
백준이는 비서에게 최대한 많은 상담을 잡으라고 부탁을 했고, 비서는 하루에 하나씩 서로 다른 사람의 상담을 잡아놓았다.
각각의 상담은 상담을 완료하는데 걸리는 기간 Ti와 상담을 했을 때 받을 수 있는 금액 Pi로 이루어져 있다.
N = 7인 경우에 다음과 같은 상담 일정표를 보자.

상담을 하는데 필요한 기간은 1일보다 클 수 있기 때문에, 모든 상담을 할 수는 없다. 예를 들어서 1일에 상담을 하게 되면, 2일, 3일에 있는 상담은 할 수 없게 된다. 2일에 있는 상담을 하게 되면, 3, 4, 5, 6일에 잡혀있는 상담은 할 수 없다.1일에 잡혀있는 상담은 총 3일이 걸리며, 상담했을 때 받을 수 있는 금액은 10이다. 5일에 잡혀있는 상담은 총 2일이 걸리며, 받을 수 있는 금액은 15이다.
또한, N+1일째에는 회사에 없기 때문에, 6, 7일에 있는 상담을 할 수 없다.
퇴사 전에 할 수 있는 상담의 최대 이익은 1일, 4일, 5일에 있는 상담을 하는 것이며, 이때의 이익은 10+20+15=45이다.
상담을 적절히 했을 때, 백준이가 얻을 수 있는 최대 수익을 구하는 프로그램을 작성하시오.
출력
첫째 줄에 백준이가 얻을 수 있는 최대 이익을 출력한다.
풀이
해당 문제는 DP, DFS 두가지 방식으로 풀이하였습니다.
첫번째 DP를 이용한 문제풀이 입니다.
1일 부터 DP 배열을 채우려고하니까 잘 풀리지 않았는데, 마지막 날짜로부터 DP 배열을 배우니 쉽게 해결할 수 있었습니다.
dp 배열을 아래와 같이 정의하겠습니다.
dp[x] : x일부터 N일까지 일했을 때 얻을 수 있는 최대 수익
이때 dp[x]는 max(P[x] + dp[x + T[x]], dp[x + 1])로 구할 수 있습니다.
P[x] + dp[x + T[x]]는 해당 날짜(x일)에 상담을 진행하는 경우
dp[x + 1]는 해당 날짜(x일)에 상담을 진행하지 않는 경우입니다.
dp[1]까지 구하면 dp[1]이 정답이 됩니다.(1일부터 N일까지 일했을 때 얻을 수 있는 최대 수익)
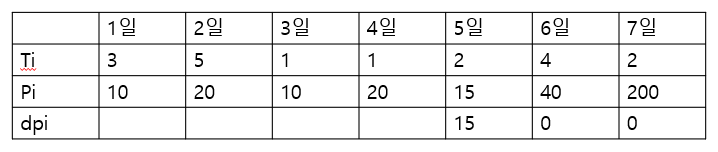
다음과 같은 상황에서 dp[4]를 구해보겠습니다.

4일에 상담을 진행하는 경우 35원을, 4일에 상담을 진행하지 않는 경우 15원을 얻을 수 있기 때문에4일에 상담을 진행하는 경우 더 많은 돈을 벌 수 있습니다.

다음과 같은 상황에서 dp[2]를 구해보겠습니다.

2일에 상담을 진행하는 경우 20원을, 2일에 상담을 진행하지 않는 경우 45원을 얻을 수 있기 때문에
2일에 상담을 진행하지 않는 경우 더 많은 돈을 벌 수 있습니다.

dp[1]까지 채우면 위와 같고 dp[1]이 정답이 됩니다.
두번째 DFS를 이용한 문제풀이 입니다.
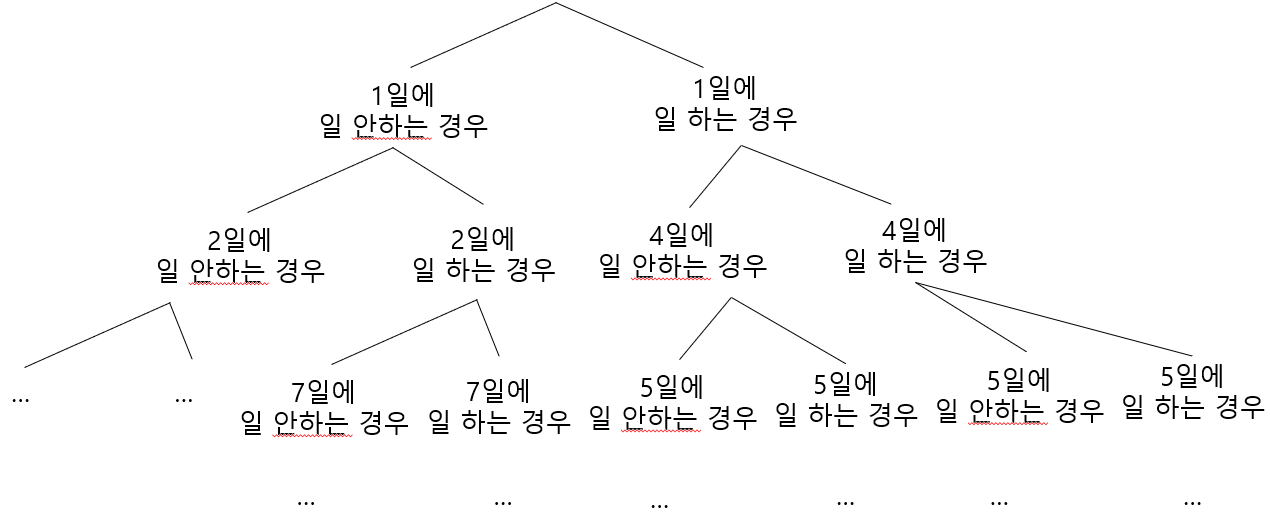
N의 범위가 크지 않기 때문에 완전탐색을 이용하여 풀이할 수 있습니다.
각 케이스에 대해 두가지 경우의 수가 존재합니다.
* 해당 일자에 일하는 경우
dfs(day + T[day], money + P[day]);
* 해당 일자에 일하지 않는 경우
dfs(day + 1, money);
그림으로 표현하면 아래와 같습니다.
전체 코드는 아래와 같습니다.
#include <iostream>
using namespace std;
int N;
int answer = 0;
const int MAX = 20;
int T[MAX];
int P[MAX];
void dfs(int day, int money) {
if (day > N) {
if (answer < money) answer = money;
}
else {
if (day + T[day] <= N + 1) {
// 해당 날짜에 일 하는 경우
dfs(day + T[day], money + P[day]);
}
// 해당 날짜에 일 안하는 경우
dfs(day + 1, money);
}
}
int main() {
cin >> N;
for (int i = 1; i <= N; i++) {
cin >> T[i] >> P[i];
}
dfs(1, 0);
cout << answer;
return 0;
}'Algorithm' 카테고리의 다른 글
| [C++][SW Expert Academy] 점심 식사시간 (0) | 2021.04.16 |
|---|---|
| [C++][백준] 아맞다우산(17244) (0) | 2021.04.16 |
| [C++][백준] 구슬 탈출 2(13460) (0) | 2021.04.16 |
| [C++][백준] 마법사 상어와 토네이도(20057) (1) | 2021.04.15 |
| [C++][백준] 인싸들의 가위바위보(16986) (0) | 2021.04.15 |


